Errors in Computational Fluid Dynamics (CFD), Mesh Generation Techniques, and Mesh Quality Assessment are critical areas of study for anyone working with CFD simulations. These topics focus on the key challenges faced during CFD modeling, including how errors impact the results, how to properly create and refine computational meshes, and how to assess the quality of those meshes to ensure accurate and reliable simulation outcomes.
1. Errors in Computational Fluid Dynamics (CFD)
In CFD, errors can arise due to a variety of factors, which can affect the accuracy, reliability, and stability of the simulation results. These errors can be grouped into several categories:
Discretization Errors: These errors occur because the continuous equations governing fluid flow (e.g., Navier-Stokes equations) are approximated by discrete equations for numerical solution. The finer the discretization (smaller grid cells), the lower the discretization error.
Numerical Errors: These result from the algorithms used to solve the equations. Issues like poor convergence, round-off errors (due to limited precision), and the choice of numerical scheme can cause inaccuracies.
Modeling Errors: These occur when simplified assumptions are made in the CFD model (e.g., turbulence models, boundary conditions, or heat transfer models), which may not completely represent the physical system being simulated.
Boundary and Initial Condition Errors: Incorrect or poorly defined boundary conditions (such as inlet velocity or wall temperature) and initial conditions can lead to incorrect results.
Understanding the sources of these errors and developing strategies to minimize or eliminate them is crucial for obtaining accurate and reliable CFD simulations.
2. Mesh Generation Techniques
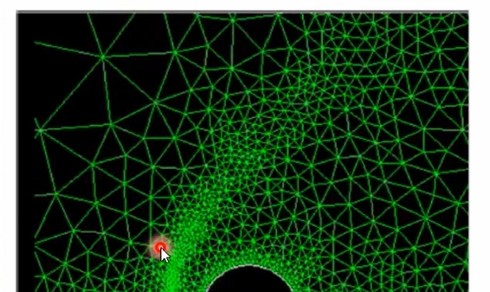
In CFD, a mesh is a discretized representation of the computational domain, and the quality of the mesh is one of the most important factors affecting the accuracy and convergence of the solution. Mesh generation techniques include:
Structured Meshes: These are regular grids where the elements (usually quadrilateral or hexahedral) are aligned along coordinate axes. They are easier to generate and solve but are limited in handling complex geometries.
Unstructured Meshes: These meshes use arbitrary shapes like triangles (2D) or tetrahedra (3D) to fill the domain. They are more flexible and can handle complex geometries, but they are computationally more expensive.
Hybrid Meshes: Combining structured and unstructured mesh techniques, hybrid meshes aim to take advantage of both methods, providing flexibility while maintaining some of the efficiency of structured grids.
Adaptive Mesh Refinement (AMR): This technique involves refining the mesh in regions with high gradients of flow variables (like velocity or temperature) to increase accuracy where needed, while coarsening the mesh in less critical areas to save computational resources.
Boundary Layer Meshes: In fluid dynamics problems with high shear stress near boundaries (e.g., walls), special attention must be paid to the boundary layer mesh, which involves finer mesh near the walls to capture the behavior of the flow.
Effective mesh generation is crucial because the mesh affects both the accuracy of the solution and the computational cost.
3. Mesh Quality Assessment
The quality of a mesh is directly linked to the accuracy and stability of the CFD solution. Poor mesh quality can lead to incorrect results, convergence issues, or unnecessarily high computational costs. Key aspects of mesh quality include:
Skewness: A measure of how much an element deviates from its ideal shape (for example, a perfect square or cube). High skewness can lead to numerical instabilities.
Orthogonality: This refers to how perpendicular the mesh cells are to each other. Poor orthogonality can lead to inaccuracies in the numerical scheme.
Aspect Ratio: This refers to the ratio of the longest to the shortest side of an element. A high aspect ratio (e.g., a very elongated element) can degrade the solution quality.
Smoothness: The smoothness of the transition between adjacent mesh elements is important. Sudden changes in mesh size or shape can cause inaccuracies in the numerical solution.
Element Size Distribution: Ideally, the mesh should have a uniform distribution of element sizes, with finer mesh areas in regions with high gradients of flow variables (like velocity or pressure). Uneven distribution can lead to computational inefficiency or inaccurate results.
Mesh quality assessment involves evaluating these parameters and applying techniques (like smoothing, refinement, or coarsening) to improve the mesh before running the simulation. Tools and algorithms exist to automatically detect and fix mesh quality issues, but they require careful attention and expertise to use effectively.